学习算法非常适合于涉及“黑盒”或多模式代价函数的流量优化和控制问题。这些算法是迭代的,通常需要比基于梯度的算法多几个数量级的代价函数评估(Bewley et al.2001)。此外,它们不提供收敛的保证,我们建议,当技术如伴随方法是适用的时候,它们是避免的。与此同时,强化学习等技术已被证明甚至比最优流量控制策略更有效(Novati等人,2019年)。正如下面所述,学习算法可能是几种流量控制和优化问题的选择方法。
与流动建模相比,优化和控制的学习算法与数据采样过程以多种方式交互。首先,根据前面章节中描述的建模工作,机器学习可以应用于开发显式的代理模型,将成本函数和控制/优化参数联系起来。替代模型,如神经网络,甚至可以适应梯度方法,尽管它们经常陷入局部最小值。多保真度算法(Perdikaris et al.2016)也可以用来将代理与完整问题的代价函数结合起来。随着学习的进行,在优化结果的指导下,需要新的数据。或者,优化或控制问题可以描述为参数的学习概率分布,使代价函数最小化。这些概率分布由优化过程中得到的代价函数样本构造而成。此外,目前用于训练非线性学习机的高维和非凸优化程序非常适合于流量控制中的高维、非线性优化问题。
我们注意到,由于强大计算机的可用性,优化和控制之间的界限正在变得模糊(见焦点框)。然而,关键时空尺度的范围和潜在过程的非线性可能会使流量控制的实时优化成为未来几十年的挑战。
1。随机流优化:学习概率分布
随机优化包括进化策略和遗传算法,它们最初是基于生物启发原理发展起来的。然而,在过去的20年里,这些算法已经被置于一个学习框架中(Kern et al.2004)。
随机优化在工程设计中得到了广泛的应用,特别是当许多工程问题涉及到“黑匣子”类型的成本函数时。一个非常简短的应用列表包括气动形状优化(Giannakoglou等人,2006年)、无人驾驶飞行器(uavi)(Hamdaoui等人,2010年)、人工游泳者的形状和运动优化(Gazzola等人,2012年;Van Rees等人,2015年),并改进了横流涡轮的功率提取(Strom等人,2017年)。我们参考Skinner和Zare-Behtash(2018)的综述文章,对基于梯度和随机的空气动力学优化算法进行了广泛的比较。
这些算法涉及大量的迭代,它们可以受益于大规模并行计算机架构。自动化的进步也促进了它们在实验中的应用(Strom等人,2017;Martin & Gharib 2018)和工业设置(Bueche等人,2002年)。我们注意到随机优化算法非常适合处理与不确定性相关的实验和工业挑战,如意外的系统行为,系统及其环境的部分描述,以及外部干扰。Hansen等人(2009)提出了一种提高进化算法在线优化燃烧室试验台能力的方法。
随机流量优化将继续受益于计算机硬件和实验技术的进步。同时,收敛性证明、可解释性和可靠性是该算法应用于流体力学问题时需要考虑的突出问题。混合算法以问题特定的方式结合随机技术和基于梯度的方法可以提供流动控制问题的最佳策略。
优化和控制:快速计算机擦除边界。优化和控制是密切相关的,随着计算机的速度越来越快,边界变得越来越模糊,正如Tsiotras & Mesbahi(2017)(195页)所总结的那样:
有趣的是,优化和控制之间的区别在很大程度上是语义和(唉!)实现相关的。如果一个人有能力在运行中快速解决优化问题来闭环,那么他就有(原则上)一个反馈控制律……因此,基于可用硬件的能力,同样的算法可以被视为解决优化或控制问题。随着更快、更有能力的计算机硬件架构的不断出现,优化和控制之间的边界将变得更加模糊。然而,当优化嵌入到反馈控制的实施中,经典的控制问题,如对模型不确定性、时滞、过程和测量噪声的鲁棒性变得至关重要,特别是对高性能的航空航天系统。”
2.机器学习的流量控制
反馈流量控制通过传感器测量的信息改变流体动力系统的行为。反馈是稳定不稳定系统、衰减传感器噪声、补偿外部干扰和模型不确定性所必需的。流动控制的挑战包括高维状态、非线性、潜在变量和时间延迟。机器学习算法已广泛应用于控制、系统识别和传感器放置。
2.1。准备神经网络控制。
神经网络在系统辨识(见第3节)和控制方面得到了极大的关注,包括在空气动力学方面的应用(Phan et al.1995)。将神经网络应用于湍流流动控制是Lee等人(1997)首创的。采用基于少数表面摩擦传感器的局部壁面法向吹风和吸力减小湍流边界层的表面摩擦阻力。基于传感器的控制律是从已知的最优全信息控制器中学习而来的,整体性能损失很小。此外,在不考虑任何驱动命令先验知识的情况下,对单层网络进行了优化,以减少表面摩阻。这两种策略都导致了一个概念上简单的地方反对派控制。其他一些研究采用了神经网络,例如相量控制(Rabault等人,2019年)甚至频率串扰。逼近任意非线性控制律的理论优势的代价是需要对许多参数进行优化。神经网络控制可能需要过多的计算或实验资源,以配置复杂的高维非线性和许多传感器和执行器。与此同时,自这些早期应用以来,神经网络的训练时间已经提高了几个数量级,这值得进一步研究它们在流量控制方面的潜力。
2.2。控制的遗传算法。
遗传算法已被应用于解决许多流量控制问题。它们要求控制律的结构是预先指定的,并且只包含少量可调参数。将遗传算法用于流体控制设计的一个例子用于后向台阶的实验混合优化(Benard et al.2016)。与神经网络控制一样,学习时间随着参数数量的增加而增加,对于具有非线性的控制器(如常线性二次律)、具有信号历史的控制器(如卡尔曼滤波器)或具有多个传感器和执行器的控制器来说,这是一个挑战,甚至是禁止的。
遗传规划已广泛应用于工程应用的主动控制(Dracopoulos 1997;弗莱明和Purshouse 2002年)和近年来在几个流量控制工厂。这包括多频率开环驱动、多输入传感器反馈和分布式控制的学习。我们参考Duriez等人(2016)对该方法的深入描述,参考Noack(2018)对植物的概述。我们注意到,大多数控制律已经获得了1000个测试评估,每一个只需要几秒钟在风洞。
3。通过强化学习进行流程控制
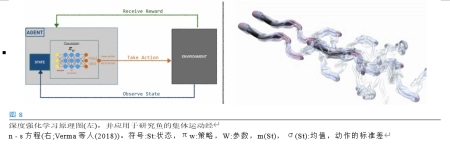
近几年RL先进领域之外的游戏,已经成为解决问题的一个基本模式在越来越多的领域,包括复制水文系统的动力学(劳克斯et al .2005),积极控制振荡层流绕流虚张声势的身体(Gueniat et al .2016年),研究个体(Gazzola等人,2014年)或鱼的集体运动(Gazzola等人,2016;Novati等人2017年;Verma et al.2018),最大化模拟滑翔机(Reddy et al.2016)和机器人滑翔机(Reddy et al.2018)的范围,优化无人机的运动学运动(Kim et al.2004;Tedrake et al.2009),并优化了微泳者的运动(Colabrese et al.2017,2018)。图8提供了一个强化学习的示意图和一个例子,展示了它在集体游泳中的应用,由Navier-Stokes方程解决。
流体力学知识对于RL的应用是必不可少的,因为成功或失败取决于正确选择状态、行动和反映流动问题控制机制的奖励。自然生物及其传感器,如鸟的视觉系统或鱼的侧线,可以指导状态的选择。随着传感器技术的快速发展,算法的挑战可能是最优的传感器布置(Papadimitriou & Papadimitriou 2015;Manohar等人,2018)。动作反映了流动驱动装置,可能涉及机体变形或翅膀拍动。奖励可能包括能量因素,比如运输成本,或者靠近鱼群中心以避免捕食。RL的计算成本仍然是它被广泛采用的一个挑战,但我们相信这个缺陷可以通过RL固有的并行性来解决。人们对可从低精度(如二维)模拟转移到高精度(如三维)模拟的方法越来越感兴趣(Verma et al.2018),或从模拟转移到相关的真实世界应用的方法(Richter et al.2016)。
评论0